The Maths of The Twelve Days of Christmas
I know this has been discussed many times over the course of the years, but I'm adding my bit, just to muddy the already opaque waters that tiny bit more.
On the first day of Christmas my true love gave to me a partridge in a pear tree.
Er, sure...
On the second day of Christmas my true love gave to me two turtle doves and a partridge in a pear tree.
Wait, "and a partridge.."?
On the third day of Christmas my true love gave to me three french hens, two [more] turtle doves and [another] partridge in a pear tree.
What's with all the partridges in pear trees?
By now I'm sure you've realised that my true love didn't just give me:
- 12 drummers drumming,
- 11 pipers piping,
- 10 lords a-leaping,
- 9 ladies dancing,
- 8 maids a-milking,
- 7 swans a-swimming,
- 6 geese a-laying,
- 5 go-old rings,
- 4 colly birds,
- 3 french hens,
- 2 turtle doves, and
- a partridge in a pear tree.
In fact that's what she gave me on just the last day. To work out how much crap she actually gave me over the course of the twelve days we can resort to Pascal's Triangle. First we draw out the triangle with thirteen or so iterations, then we highlight various diagonals, and revel in the awesomeness.
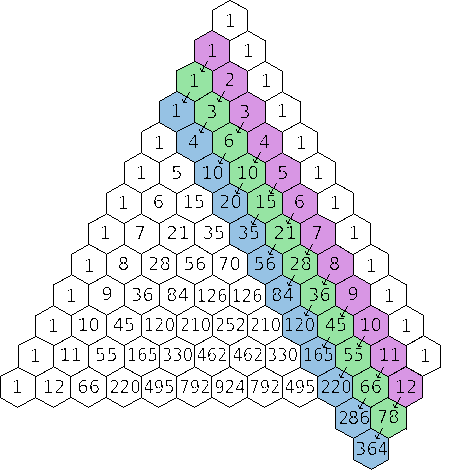
The second (purple) diagonal gives us the day of Christmas. The third (green) diagonal tells us how many gifts we received on that day. The fourth (blue) diagonal shows how many gifts we've received in total up to that day. Thus we can see that after all twelve days are up, I've received a total of 364 stupid, stupid gifts, such as jumping noblemen, bagpipe players and bloody trees with birds in and whatnot.
All that's missing is the final count of how many of each stupid gift I was given. This can be illustrated in tabular form:
| Stupid Gift | Number per Day | Number of Days | Total |
|---|---|---|---|
| partridges in pear trees | 1 | 1..12 ⇒ 12 | 12 |
| turtle doves | 2 | 2..12 ⇒ 11 | 22 |
| french hens | 3 | 3..12 ⇒ 10 | 30 |
| colly birds | 4 | 4..12 ⇒ 9 | 36 |
| gold rings | 5 | 5..12 ⇒ 8 | 40 |
| geese a-laying | 6 | 6..12 ⇒ 7 | 42 |
| swans a-swimming | 7 | 7..12 ⇒ 6 | 42 |
| maids a-milking | 8 | 8..12 ⇒ 5 | 40 |
| ladies dancing | 9 | 9..12 ⇒ 4 | 36 |
| lords a-leaping | 10 | 10..12 ⇒ 3 | 30 |
| pipers piping | 11 | 11..12 ⇒ 2 | 22 |
| drummers drumming | 12 | 12..12 ⇒ 1 | 12 |
WARNING: what follows is my train of thought, and may not necessarily be instructive, interesting, or even correct. Proceed at your peril.
Those green numbers are actually the first twelve triangular numbers. That is, if you draw a triangle with one dot on the first row, two on the second, and so on, the nth triangular number is the number of dots up to and including the nth row.

Mathematically this can be written as:
The blue numbers are the first twelve tetrahedral numbers. Those are what you get if you make a tetrahedron (like a pyramid, but with three faces instead of four), where each layer is made of the corresponding triangular number.

From the table, the formula for how many of the gift I was first given on the jth day, up to the nth, is:
So an alternative way to work out how many gifts I was given in total up to the nth day is:
...which, since it's calculating the same number as the tetrahedal formula above, implies that:
Since Gauss showed that:
...this all suggests that:
I'd like to believe that means that: but I'm not going to attempt to approach that proof at twenty past midnight. Also I'm sure there's something to do with a modulus there [ where , maybe?] but I'll leave it for another day to work out what it all means. If you can explain it in a reasonably clear and meaningful way, please leave a comment below. Our gratitude will be a wonderful reward.
PS. it's taken me 4 hours (±5 minutes) to write this. If only it was something constructive.